Département de pharmacie
Faculté de médecine
Université de Constantine 3
Faculté de médecine
Université de Constantine 3


| Département de Pharmacie | |
| Enseignants / Tuteurs | |
| Organisation Pédagogique | |
| - Programme officiel | |
| - Plan de cours | |
| - Emploi du temps | |
| - Notes de cours | |
| 1. Situation problème | |
| 2. Statistiques descriptives | |
| 3. Théorèmes fondamentaux de probabilité | |
| |
| |
| |
| |
| 8. Estimation | |
| 9. Théorie générale des tests d'hypothèse, intervalles de pari | |
| 10. Comparaisons de moyennes | |
| 11. Comparaison de proportions | |
| Ressources | |
| Projets | |
| Bibliographie |
| ESPACE PRIVÉ |
| Accées Plateforme |
| Résultats des évaluations |
 |  |
Lois des probabilités discrètes
III. Quelques lois de probabilités discrètes particulières (célèbres)
Différentes
expériences peuvent être modélisées à l’aide d’une même loi de probabilité. Il
suffit juste de reconnaitre dans un problème donné, la structure (ou loi)
probabiliste qu’il est convenable d’appliquer.
Dans ce qui suit, nous
allons examiner les modèles discrètes les plus souvent utilisés en pratique,
qu’elles sont leurs principales propriétés et comment les reconnaitre dans un
problème donné.
1. Loi de Bernouilli
Dans le modèle de loi de Bernoulli, l’expérience
ne peut donner lieu qu’à deux résultats : succès ou échec. Ainsi, la variable aléatoire qui nous intéresse
prendra la valeur 1 si on a obtenu un succès et 0 si c’est le cas contraire
donc un échec.
En posant la probabilité de succès égale à p, on peut définir une variable aléatoire de Bernoulli de la manière suivante.
En posant la probabilité de succès égale à p, on peut définir une variable aléatoire de Bernoulli de la manière suivante.
1.1. Définition
1.2. Caractéristiques de la loi de Bernouilli
Démonstration
E(Y)=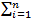 yi . Pr (Y = yi) = 0. (1- π) + 1. π
= π
yi . Pr (Y = yi) = 0. (1- π) + 1. π
= π
E(Y2)=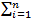 yi2 . Pr (Y = yi) = 02. (1- π) + 12. π
= π
yi2 . Pr (Y = yi) = 02. (1- π) + 12. π
= π
Var (Y) = E(Y2) - E(Y)2 = π - π2 = π . (1 - π)
La variable aléatoire Y = «avoir une insuffisance rénale» suit une loi de Bernoulli de paramètre π = 0,1 : Y = (1 ; 0,1)
E(Y) = π = 0,1
Var(Y) = π.(1- π) = 0,1 . (1 – 0,1) = 0,09
Soit une expérience aléatoire ayant deux
résultats possibles :
E= {le succès} et E*= {l’échec}
On associe à cette épreuve une variable aléatoire discrète Y ayant deux réalisations possibles:
Y = { 0, 1} avec :
Y ~ B (1 ; π )
Dans certains livres on peut trouver aussi la notation : Y ~ Bernoulli (p)
E= {le succès} et E*= {l’échec}
On associe à cette épreuve une variable aléatoire discrète Y ayant deux réalisations possibles:
Y = { 0, 1} avec :
- Y=1 associé à un succès avec Pr(E) = Pr(Y=1) = π
- Y=0 associé à un échec avec Pr(E*) = Pr(Y=0) = 1-π
- et avec 0 ≤ π ≤ 1
Y ~ B (1 ; π )
Dans certains livres on peut trouver aussi la notation : Y ~ Bernoulli (p)
1.2. Caractéristiques de la loi de Bernouilli
| Paramètres caractéristiques : Y ~ B (1 ; π) | |
| Réalisations | Y = 0 ou 1 (discrète finie) |
| Probabilités | Pr(Y=1) = π avec 0 ≤ π ≤ 1 Pr(Y=0)= 1- π |
| Espérance | E(Y) = π |
| Variance | Var(Y) = π.(1- π) |
| Écart-type | σ(Y) = |
Démonstration
| yi | 0 | 1 |
| Pr(Y=yi) | 1- π | π |
E(Y)=
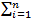 yi . Pr (Y = yi) = 0. (1- π) + 1. π
= π
yi . Pr (Y = yi) = 0. (1- π) + 1. π
= πE(Y2)=
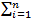 yi2 . Pr (Y = yi) = 02. (1- π) + 12. π
= π
yi2 . Pr (Y = yi) = 02. (1- π) + 12. π
= πVar (Y) = E(Y2) - E(Y)2 = π - π2 = π . (1 - π)
Exemple 16
La variable aléatoire Y = «avoir une insuffisance rénale» suit une loi de Bernoulli de paramètre π = 0,1 : Y = (1 ; 0,1)
E(Y) = π = 0,1
Var(Y) = π.(1- π) = 0,1 . (1 – 0,1) = 0,09


