Département de pharmacie
Faculté de médecine
Université de Constantine 3
Faculté de médecine
Université de Constantine 3
| Département de Pharmacie | |
| Enseignants / Tuteurs | |
| Organisation Pédagogique | |
| - Programme officiel | |
| - Plan de cours | |
| - Emploi du temps | |
| - Notes de cours | |
| 1. Situation problème | |
| 2. Statistiques descriptives | |
| 3. Théorèmes fondamentaux de probabilité | |
| |
| |
| |
| |
| 8. Estimation | |
| 9. Théorie générale des tests d'hypothèse, intervalles de pari | |
| 10. Comparaisons de moyennes | |
| 11. Comparaison de proportions | |
| Ressources | |
| Projets | |
| Bibliographie |
| ESPACE PRIVÉ |
| Accées Plateforme |
| Résultats des évaluations |
 |  |
Lois des probabilités discrètes
5.6. Théorèemes importants
1. Soit une variable aléatoire X telle que E(X) = µ et Var (X) = σ2
Si on considère la transformation linéaire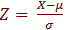
(la cote Z de X), on a alors
E(Z) = 0 et Var (Z) = 1
2. Soit une suite de variables aléatoires X1, X2,.., Xn indépendantes, de mêmes moyennes et de même variances, autrement dit : E(Xi) = µ et Var(Xi) = σ2 pour i=1,..,n
Si on considère la variable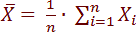
alors on a:
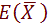= µ et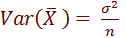 
Démonstration
1. Soit une variable aléatoire X telle que E(X) = µ, Var (X) = σ2 et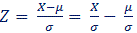
Sachant que : E(aX+b)= a E(X) + b et E(X-Y) = E(X) - E(Y)
Alors : E(Z) = E ( z / σ - µ / σ ) = 1/ σ . E(X) - µ / σ = µ / σ - µ / σ = 0
et Var(Z) = Var ( X / σ - µ / σ ) = 1 / σ2 . Var (X) = σ2 / σ2 = 1
2. On a
où les variables sont indépendantes avec E(Xi) = µ et Var(Xi)= σ2
En utilisant toujours les propriétés sur les moyennes et les variables aléatoires, on obtient alors
E(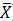
) = E ( 1/n . 
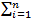Xi ) = 1/n . 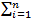E(Xi) = 1/n . 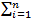µ = n . µ / n = µ
et
Var (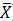) = Var ( 1/n . 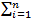Xi ) = 1/n2 . 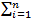Var (Xi ) = 1/n2 . 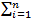σ2 = σ2/n
Soit k ϵ IR et X une variable aléatoire. On a alors:
Pr ( µ - k.σ ≤ X ≤ µ + k.σ ) ≥ 1 - 1 / k2
5.6.1. Théorème 1
1. Soit une variable aléatoire X telle que E(X) = µ et Var (X) = σ2
Si on considère la transformation linéaire
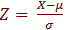(la cote Z de X), on a alors E(Z) = 0 et Var (Z) = 1
2. Soit une suite de variables aléatoires X1, X2,.., Xn indépendantes, de mêmes moyennes et de même variances, autrement dit : E(Xi) = µ et Var(Xi) = σ2 pour i=1,..,n
Si on considère la variable
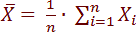alors on a: 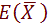= µ et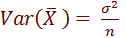 Démonstration
1. Soit une variable aléatoire X telle que E(X) = µ, Var (X) = σ2 et
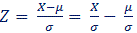
Sachant que : E(aX+b)= a E(X) + b et E(X-Y) = E(X) - E(Y)
Alors : E(Z) = E ( z / σ - µ / σ ) = 1/ σ . E(X) - µ / σ = µ / σ - µ / σ = 0
et Var(Z) = Var ( X / σ - µ / σ ) = 1 / σ2 . Var (X) = σ2 / σ2 = 1
2. On a
où les variables sont indépendantes avec E(Xi) = µ et Var(Xi)= σ2 En utilisant toujours les propriétés sur les moyennes et les variables aléatoires, on obtient alors
E(
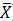) = E ( 1/n . 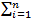Xi ) = 1/n . 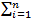E(Xi) = 1/n . 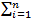µ = n . µ / n = µet
Var (
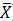) = Var ( 1/n . 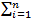Xi ) = 1/n2 . 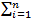Var (Xi ) = 1/n2 . 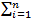σ2 = σ2/nSoit k ϵ IR et X une variable aléatoire. On a alors:
Pr ( µ - k.σ ≤ X ≤ µ + k.σ ) ≥ 1 - 1 / k2
Exemple 15
Soit la variable
aléatoire qui représente le poids (en kg) d’un appareil produit par une chaine
de montage et supposons que E(X)=75
et Var (X)=16.
Quelle est la
probabilité pour que les appareils produits aient un poids compris entre 67kg
et 83kg.
Solution
µ-k.σ = 67 à
k = (µ- 67)/ σ = (75-67)/4 = 2
Pr
(75 – 2. 4 ≤ X ≤ 75 + 2. 4) ≥ 1-1/ 22
 |  |  |