Département de pharmacie
Faculté de médecine
Université de Constantine 3
Faculté de médecine
Université de Constantine 3
| Département de Pharmacie | |
| Enseignants / Tuteurs | |
| Organisation Pédagogique | |
| - Programme officiel | |
| - Plan de cours | |
| - Emploi du temps | |
| - Notes de cours | |
| 1. Situation problème | |
| 2. Statistiques descriptives | |
| 3. Théorèmes fondamentaux de probabilité | |
| |
| |
| |
| |
| 8. Estimation | |
| 9. Théorie générale des tests d'hypothèse, intervalles de pari | |
| 10. Comparaisons de moyennes | |
| 11. Comparaison de proportions | |
| Ressources | |
| Projets | |
| Bibliographie |
| ESPACE PRIVÉ |
| Accées Plateforme |
| Résultats des évaluations |
 |  |
Lois des probabilités discrètes
5.4. Ecart-type
L’’écart-type de la variable aléatoire X, noté σ (X) est la racine carrée de la variance:
σ(X) =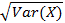
L’écart-type exprime également la dispersion de la variable aléatoire.
Exemple 11
On lance un dé régulier à six faces et on noter le numéro de la face obtenue. Les événements élémentaires sont donc équiprobables.
Calculer Fx(x), E(X), Var(X), σ(X), Pr(X ≤ 3).
Solution
Fx(x) = Pr(X ≤ x)
E(X) =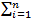
xi . pi = 1(1/6) + 2 (1/6) + 3(1/6) + 4(1/6) + 5(1/6) + 6(1/6) = 3,5
Var(X) = E(X2) - E(X)2 = 12(1/6) + 22(1/6) + 32(1/6) + 42(1/6) + 52(1/6) + 62(1/6) - 3,52 = 2,9167
σ(X) =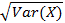 = 2,91671/2 = 1,7078
Pr(X ≤ 3) = Fx(3) = Pr(X = 1) + Pr(X = 2) + Pr(X = 3) = 1/6 + 1/6 + 1/6 = 3/6 = 0,5
Exemple 13 (Suite de l’exemple 9)
La loi de probabilité de la variable aléatoire X, nombre de souris présentant une réaction allergique au vaccin, soit donnée par le tableau de correspondance suivant :
Calculer E(X), Var (X), σ (X) , Fx(x), Mo(X)
Solution
E(X) =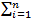xi . pi = 0(0,6561) + 1 (0,2916) + 2(0,0486) + 3(0,0036) + 4(0,0001) = 0,4
Var(X) = E(X2) - E(X)2 = 02.(0,6561) + 12 .(0,2916) + 22.(0,0486) + 32.(0,0036) + 42.(0,0001)- 0,42 = 0,36
σ(X) =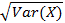 = 0,361/2 = 0,6
Mo(X) = 0
Exemple 14
Le tableau suivant présente les moyennes et les variances de 4 variables aléatoires indépendantes.
b) Y2 = X1 + X2 - 3. X3 + 2. X4
Solution
Sachant que : E(X+Y) = E(X) + E(Y) et Var (X+Y) = Var (X) + Var (Y)
a) E(Y1) = E(X1 + X2) = E(X1)+ E(X2) = 7 + 3 = 10
Var(Y1)=Var(X1 + X2) = Var(X1) + Var(X2) = 4 + 9 = 13
b) E(Y2) = E(X1 + X2 - 3. X3 + 2. X4) = E(X1) + E(X2)- 3. E(X3)+ 2. E(X4) = 7 + 3 – 3(0) +2(-1) = 8
Var(Y2)= Var (X1 + X2 - 3. X3 + 2. X4) = Var (X1) + Var (X2)+ (– 3)2. .Var (X3)+ 22. Var (X4) = = 4 + 9 + 9.(0,25) + 4(8) = 47,25
L’’écart-type de la variable aléatoire X, noté σ (X) est la racine carrée de la variance:
σ(X) =
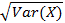
L’écart-type exprime également la dispersion de la variable aléatoire.
Exemple 11
On lance un dé régulier à six faces et on noter le numéro de la face obtenue. Les événements élémentaires sont donc équiprobables.
| X | 1 | 2 | 3 | 4 | 5 | 6 | Total |
| Pr(X=xi) | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 | 1 |
Solution
Fx(x) = Pr(X ≤ x)
E(X) =
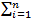xi . pi = 1(1/6) + 2 (1/6) + 3(1/6) + 4(1/6) + 5(1/6) + 6(1/6) = 3,5Var(X) = E(X2) - E(X)2 = 12(1/6) + 22(1/6) + 32(1/6) + 42(1/6) + 52(1/6) + 62(1/6) - 3,52 = 2,9167
σ(X) =
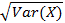= 2,91671/2 = 1,7078Pr(X ≤ 3) = Fx(3) = Pr(X = 1) + Pr(X = 2) + Pr(X = 3) = 1/6 + 1/6 + 1/6 = 3/6 = 0,5
5.5. Mode
Le mode de la variable aléatoire X, noté Mo(X), est
la (ou les) valeur(s) de la réalisation de X qui a (ont) la plus grande
probabilité de réalisation :
Pr(X = Mo(X)) ≥ Pr(X = xi)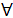 
xi
Le problème de l’insuffisance rénale. La variable
aléatoire associée est Y.
| yi | 0 | 1 |
| Pr (Y =yi ) | 0,9 | 0,1 |
Mo(Y) = 0 puisque Pr(Y=0) ≥ Pr(Y=1)
Exemple 13 (Suite de l’exemple 9)
La loi de probabilité de la variable aléatoire X, nombre de souris présentant une réaction allergique au vaccin, soit donnée par le tableau de correspondance suivant :
| xi | 0 | 1 | 2 | 3 | 4 |
| pi | 0,6561 | 0,2916 | 0,0486 | 0,0036 | 0,0001 |
Calculer E(X), Var (X), σ (X) , Fx(x), Mo(X)
Solution
E(X) =
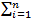xi . pi = 0(0,6561) + 1 (0,2916) + 2(0,0486) + 3(0,0036) + 4(0,0001) = 0,4Var(X) = E(X2) - E(X)2 = 02.(0,6561) + 12 .(0,2916) + 22.(0,0486) + 32.(0,0036) + 42.(0,0001)- 0,42 = 0,36
σ(X) =
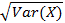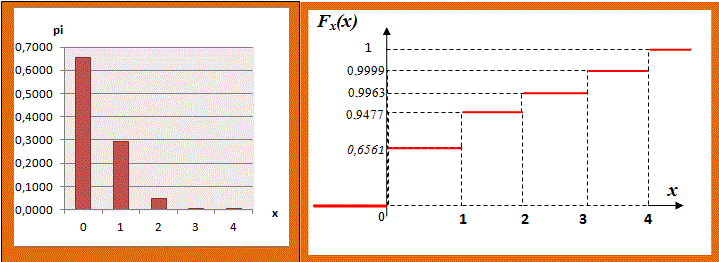
= 0,361/2 = 0,6| x | Fx(x) = Pr (X ≤ xi) |
| x < 0 | 0 |
| 0 ≤ x < 1 | Pr(X=0) = 0,6561 |
| 1 ≤ x < 2 | Pr(X=0) + Pr(X=1) =0,9477 |
| 2 ≤ x < 3 | Pr(X=0) + Pr(X=1) + Pr(X=2) = 0,9963 |
| 3 ≤ x < 4 | Pr(X=0) + Pr(X=1) + Pr(X=2) + Pr(X=3) = 0,9999 |
| x ≥ 4 | Pr(X=0) + Pr(X=1) + Pr(X=2) + Pr(X=3) + Pr(X=4) = 1 |
Mo(X) = 0
Exemple 14
Le tableau suivant présente les moyennes et les variances de 4 variables aléatoires indépendantes.
| Variable | X1 | X2 | X3 | X4 |
| Moyenne | 7 | 3 | 0 | -1 |
| Variance | 4 | 9 | 0,25 | 8 |
Calculer la moyenne et
la variance des variables aléatoires suivantes :
b) Y2 = X1 + X2 - 3. X3 + 2. X4
Solution
Sachant que : E(X+Y) = E(X) + E(Y) et Var (X+Y) = Var (X) + Var (Y)
a) E(Y1) = E(X1 + X2) = E(X1)+ E(X2) = 7 + 3 = 10
Var(Y1)=Var(X1 + X2) = Var(X1) + Var(X2) = 4 + 9 = 13
b) E(Y2) = E(X1 + X2 - 3. X3 + 2. X4) = E(X1) + E(X2)- 3. E(X3)+ 2. E(X4) = 7 + 3 – 3(0) +2(-1) = 8
Var(Y2)= Var (X1 + X2 - 3. X3 + 2. X4) = Var (X1) + Var (X2)+ (– 3)2. .Var (X3)+ 22. Var (X4) = = 4 + 9 + 9.(0,25) + 4(8) = 47,25
 |  |  |