Faculté de médecine
Université de Constantine 3


| Département de Pharmacie | |
| Enseignants / Tuteurs | |
| Organisation Pédagogique | |
| - Programme officiel | |
| - Plan de cours | |
| - Emploi du temps | |
| - Notes de cours | |
| 1. Situation problème | |
| 2. Statistiques descriptives | |
| 3. Théorèmes fondamentaux de probabilité | |
| |
| |
| |
| |
| 8. Estimation | |
| 9. Théorie générale des tests d'hypothèse, intervalles de pari | |
| 10. Comparaisons de moyennes | |
| 11. Comparaison de proportions | |
| Ressources | |
| Projets | |
| Bibliographie |
| ESPACE PRIVÉ |
| Accées Plateforme |
| Résultats des évaluations |
 |  |
Lois des probabilités discrètes
5.3.1. Définition
La variance de la variable aléatoire X, notée Var(X) est le moment centré d’ordre 2, c'est-à-dire l’espérance mathématique du carré de la variable aléatoire centrée.
Var (X) = E( [X - E(X )]2) =
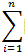 [xi - E(X)]2 . Pr ( X = xi )
[xi - E(X)]2 . Pr ( X = xi )La variance est d’autant plus faible que
les écarts à la moyenne sont faible (c’est-à-dire que les [xi
– E(X)] sont faibles). La variance est un indicateur de
dispersion d’une variable aléatoire autour de son espérance mathématique
5.3.2. Théorème de Kôning
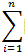 xi2 . Pr (X=xi ) - (
xi2 . Pr (X=xi ) - ( 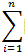 xi . Pr(X=xi) )2 = E(X2) - [E(X)]2
xi . Pr(X=xi) )2 = E(X2) - [E(X)]2Démonstration
Var(X) = E ( [X – E(X)]2
) = E ( X2 – 2 X. E(X) +
[E(X)]2 )
= E(X2) – 2. E(X). E(X)
+ [E(X)]2 = E(X2) -
[E(X)]2
Exemple 10 (Suite de l’exemple 9)
Le
problème de l’insuffisance rénale. La variable aléatoire associée est Y.
| yi | 0 | 1 |
| Pr (Y =yi ) | 0,9 | 0,1 |
Calculer Var (Y)
Solution
Var (Y) = E(Y2) - [E(Y)]2 = 0,1 – 0,12 = 0,09
| Var(X) ≥ 0 Var(a) = 0 Var (a.X) = a2 . Var(X) Var (X+a) = Var (X) |
2. Si X et Y sont deux variables aléatoires indépendantes alors :
|
Var (X+Y) = Var (X) + Var (Y) Var (X – Y) = Var (X) + Var (Y) |
Forme générale
Var ( 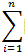 ai .Xi + bi ) = ai .Xi + bi ) = 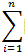 ai2 . Var (Xi) ai2 . Var (Xi) |
Démonstrations
1. Var (aX) = E(a2.X2) – E(a.X)2 = a2.[E(X2)-E(X)2] = a2. Var(X)
2. Var(X+a) = E[(X+a)2] - E(X+a)2 =
E(X2 + a2 + 2.a.X] - E(X+a)2
= E(X2) + a2 + 2.a. E(X) – (E(X) + a)2
= E(X2) + a2 + 2.a. E(X) – E(X)2 – a2
- 2.a. E(X)
3. Var(X-Y) = Var(X)+Var(-Y) = Var(X)+(-1)2.Var(Y) = Var(X) + Var(Y)


