Département de pharmacie
Faculté de médecine
Université de Constantine 3
Faculté de médecine
Université de Constantine 3


| Département de Pharmacie | |
| Enseignants / Tuteurs | |
| Organisation Pédagogique | |
| - Programme officiel | |
| - Plan de cours | |
| - Emploi du temps | |
| - Notes de cours | |
| 1. Situation problème | |
| 2. Statistiques descriptives | |
| 3. Théorèmes fondamentaux de probabilité | |
| |
| |
| |
| |
| 8. Estimation | |
| 9. Théorie générale des tests d'hypothèse, intervalles de pari | |
| 10. Comparaisons de moyennes | |
| 11. Comparaison de proportions | |
| Ressources | |
| Projets | |
| Bibliographie |
| ESPACE PRIVÉ |
| Accées Plateforme |
| Résultats des évaluations |
 |  |
Lois des probabilités discrètes
5. Paramètres caractéristiques de la variable aléatoire
Les définitions des paramètres caractéristiques sont données pour un ensemble dénombrable fini (donc allant de 1 à n fini). Ces définitions peuvent être généralisées pour un ensemble dénombrable infini en remplaçant n par ∞.
5.1. Espérance mathématique
L’espérance de la variable aléatoire X, notée E(X), est la somme des réalisations possibles pondérées par leurs probabilités respectives.
E(X) =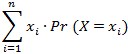 =
= 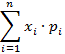
L’espérance est un paramètre de position (moyenne pondérée) de la variable aléatoire.
1. Soient variables aléatoires X et Y et deux réels a et b
2. Si E(X) = 0, on dit que la variable aléatoire est centrée
5.2. Moment d'ordre r
Exemple 9 (Suite de l’exemple 2)
Calculer le moment d’ordre 2 de cette variable Y.
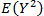 =
= 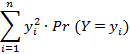 =
= 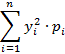 = 02 + 12 . 0,9 + 12 . 0,1 = 0,1
= 02 + 12 . 0,9 + 12 . 0,1 = 0,1
5.1.1. Définition
L’espérance de la variable aléatoire X, notée E(X), est la somme des réalisations possibles pondérées par leurs probabilités respectives.
E(X) =
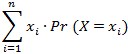 =
= 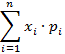
L’espérance est un paramètre de position (moyenne pondérée) de la variable aléatoire.
1. Soient variables aléatoires X et Y et deux réels a et b
|
E(a)=a E(aX+b)= a E(X) + b E(X+Y) = E(X) + E(Y) E(X-Y) = E(X) - E(Y) |
2. Si E(X) = 0, on dit que la variable aléatoire est centrée
5.2. Moment d'ordre r
Le moment d’ordre r
d’une variable aléatoire X, notée E(Xr)
est défini par :
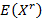 =
= 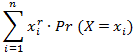 =
= 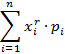
Si r=2, on parle de
moment d’ordre 2
Exemple 9 (Suite de l’exemple 2)
Le
problème de l’insuffisance rénale. La variable aléatoire associée est Y.
| yi | 0 | 1 |
| Pr (Y =yi ) | 0,9 | 0,1 |
Calculer le moment d’ordre 2 de cette variable Y.
Solution
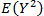 =
= 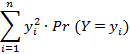 =
= 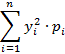 = 02 + 12 . 0,9 + 12 . 0,1 = 0,1
= 02 + 12 . 0,9 + 12 . 0,1 = 0,1

