Faculté de médecine
Université de Constantine 3


| Département de Pharmacie | |
| Enseignants / Tuteurs | |
| Organisation Pédagogique | |
| - Programme officiel | |
| - Plan de cours | |
| - Emploi du temps | |
| - Notes de cours | |
| 1. Situation problème | |
| 2. Théorèmes fondamentaux de probabilité | |
| 3. Lois de probabilités discrête | |
| |
| |
| |
| |
| 8. Estimation | |
| 9. Théorie générale des tests d'hypothèse, intervalles de pari | |
| 10. Comparaisons de moyennes | |
| 11. Comparaison de proportions | |
| Ressources | |
| Projets | |
| Bibliographie |
| ESPACE PRIVÉ |
| Accées Plateforme |
| Résultats des évaluations |
 |  |
Théorèmes fondamentaux des probabilités
§ Si E
est fini, ou infini dénombrable, tout sous-ensemble de E est un
événement ; ce n’est pas vrai si E est non dénombrable (ceci sort du cadre
de ce cours).
§ On note parfois
Ω l’ensemble
de tous les événements, c’est l’ensemble P(E) des parties de E.
§ Lorsqu’une
épreuve mène à n événements élémentaires possibles, on peut construire à partir
d’eux 2n
événements
Exemple 8
1)
On jette une pièce de monnaie et on observe le
résultat obtenu.
L’ensemble fondamental est formé par les
combinaisons suivantes : E= {P, F}.
Dans ce cas, Ω = P(E) = { Ø, {P},{F},{P, F}}
Card(Ω) = 22 = 4 on peut donc construire 4 événements.
L’ensemble
fondamental est formé par les 6 résultats possibles : E={1, 2, 3, 4, 5,
6}.
L’événement
correspondant à l’apparition d’un nombre pair est A = {2,
4, 6}, qui est bien un sous ensemble de
E.
L’événement
correspondant à l’apparition d’un nombre premier est B = {1,
2, 3, 5} et l’événement correspondant à
l’apparition d’un 3 est C = {3}.
Dans ce cas du dé, il y a 26 =64 parties possibles.
On jette une pièce de monnaie jusqu’à ce qu’on obtienne pile ; l’ensemble fondamental correspondant est la suite des nombres entiers E = {1, 2, 3, ..., n, ...} puisqu’on peut avoir un pile au bout d’un jet, de 2 jets, de n jets, n étant aussi grand que l’on veut.
4)
On vise avec une fléchette une cible suffisamment
grande ; si on admet que la fléchette est très fine, comme le serait un
point de la géométrie, l’espace fondamental est la surface de la cible qui est
constituée de points et donc infinie et non dénombrable.
6. Opérations sur les événements
Les événements peuvent se combiner entre eux pour former de nouveaux événements. Si A et B sont deux événements, les opérations possibles à partir de A et B sont :
1. 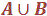 est l’événement qui se
produit si A ou B (ou les deux) est réalisé.
est l’événement qui se
produit si A ou B (ou les deux) est réalisé.
Il est parfois noté 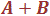 ou A ou B.
ou A ou B.
2. 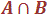 est l’événement qui se
produit si A et B sont réalisés tous les deux.
est l’événement qui se
produit si A et B sont réalisés tous les deux.
Il
est parfois noté 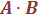 ou A et B.
ou A et B.
3. 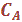 est l’événement qui se
produit quand A n’est pas réalisé. On l’appelle aussi négation de A.
La liste d’événement complémentaires qui le définit est donc composée de tous les éléments de E qui n’appartiennent
pas à la liste de A.
est l’événement qui se
produit quand A n’est pas réalisé. On l’appelle aussi négation de A.
La liste d’événement complémentaires qui le définit est donc composée de tous les éléments de E qui n’appartiennent
pas à la liste de A.
Il est parfois noté « non A » ou 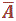 .
.
4. On
dit que l’événement A implique l’événement B (ou encore 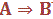 ) si
) si 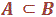
5. Événement
incompatibles : Quand deux événements A et B
sont tels que 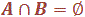 , ils ne peuvent être réalisés simultanément.
On dit qu’ils s’excluent mutuellement, ou qu’ils sont incompatibles.
, ils ne peuvent être réalisés simultanément.
On dit qu’ils s’excluent mutuellement, ou qu’ils sont incompatibles.
6. Systèmes complet d’événements : On dit que les événements A1, A2, … , An forment une famille complète si les Ai constituent une partition de E, c’est-à-dire si :
i) les
événements sont deux à deux disjoints :
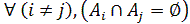
ii) ils
couvrent tout l’espace :
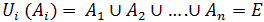
 |  |  |